티스토리 뷰
[디자인 연구 방법론 - chi-square test] 1. frequency 비교
익명132 2020. 10. 2. 16:04비교와 관련된 통계 분석 방법들을 알아보려고 한다.
parametric statistics 중 chi-square test을 알아본다.
chi-square test: 그룹 간의 차이를 chi-square 분포를 사용해서 가설검정하는 것이다.
independent variable과 dependent variable이 모두 categorical variable인 경우, 교차표(cross tabulation table)을 사용해서 분석할 수 있다.
chi-square test를 이용한 3가지의 다른 가설을 가진 테스트들을 확인해보려 한다. (유의 수준 0.05로 고정)
chi-square 값은 관찰 빈도와 기대 빈도의 차이를 기대 빈도로 나눈 것이다.
즉, 0에 가까울 수록 기대 빈도와 가깝다는 것이다. 식으로는 아래와 같다. ($f_{o}$: 관찰 빈도, $f_{e}$: 기대 빈도 )
$X^{2} = \sum \frac{(f_{o}-f_{e})^{2}}{f_{e}}$
Goodness-of-fit test
1개의 population과 1개의 categorical variable을 가진다.
$H_{0}$(null hypothesis): 각 카테고리의 비율이 특정한 분포를 가진다.
$H_{1}$(alternative hypothesis): 각 카테고리의 비율이 특정한 분포에 일치하지 않는다.
한 개의 variable을 가지기 때문에, 교차 분할표를 사용하지 않는다. (One-way)
따라서 자유도는 아래와 같이 구한다.
d.f. (degree of freedom): number of category(K) -1
사람들이 좋아하는 음식 종류는 1:1:1이 맞을까?
| Row total | |
| 닭발 | 7 |
| 치킨 | 5 |
| 국밥 | 6 |
| Column total | 18 |
$E_{i} = n * p_{i}
E_{1} = 18 * \frac{1}{3}
E_{2} = 18 * \frac{1}{3}
E_{3} = 18 * \frac{1}{3}$
$X^{2} = \frac{(7-6)^{2}}{6} + \frac{(5-6)^{2}}{6} + \frac{(6-6)^{2}}{6}$ = 0.33
d.f. = 3 -1
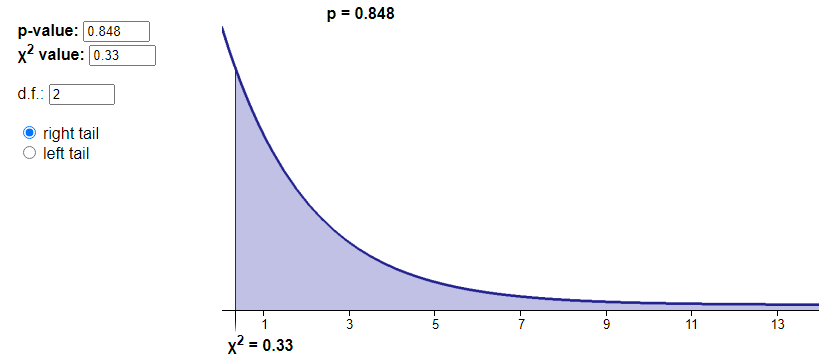
$\therefore$ p 값(0.848)이 유의 수준(0.05) 보다 크므로 null hypothesis를 채택한다. 이 실험에서 사람들은 1:1:1의 비율로 음식을 좋아하고 있다.
Test of Homogeneity
2개 이상의 population (혹은 population의 subgroup)과 1개의 categorical variable을 가진다.
$H_{0}$: 모든 카테고리의 분포는 같다.
$H_{1}$: 분포에 차이가 있다.
두 개의 variable에서 나온 조합으로 교차 분할표를 작성한다. (Two-way)
따라서 자유도는 아래와 같이 구한다.
d.f. : (number of rows -1) * (number of columns -1)
여자가 가장 좋아하는 음식 종류와, 남자가 가장 좋아하는 음식 종류는 같은 분포를 가질까?
| 여자 | 남자 | Row total | |
| 닭발 | 5 | 2 | 7 |
| 치킨 | 3 | 2 | 5 |
| 국밥 | 1 | 5 | 6 |
| Column total | 9 | 9 | 18 |
$E_{r,c} = (n_{r} * n_{c}) / n
E_{1,1} = (7*9) / 18 = 3.5
E_{1,2} = (7*9) / 18 = 3.5
E_{2,1} = (5*9) / 18 = 2.5
E_{2,2} = (5*9) / 18 = 2.5
E_{3,1} = (6*9) / 18 = 3
E_{3,2} = (6*9) / 18 = 3
X^{2} = (5 - 3.5)^{2} + (2 - 3.5)^{2} + (3 - 2.5)^{2} + (2 - 2.5)^{2} + (1 - 3)^{2} + (5 - 3)^{2} = 13
d.f = (3-1) * (2-1) = 2
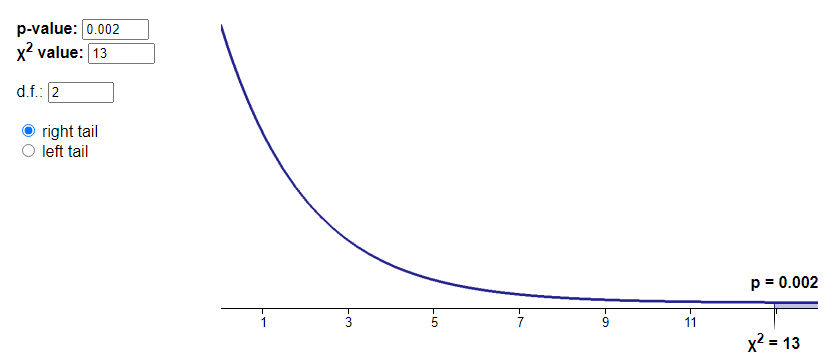
$\therefore$ p 값(0.002)이 유의수준(0.05)보다 작으므로 null hypothesis를 채택할 수 없다. 이 실험에서 여자와 남자가 좋아하는 음식의 분포는 차이가 존재한다.
Test of Independence
1개의 population과 2개의 categorical variable을 가진다.
$H_{0}$: 2개의 variable은 연관성이 없다. 즉, (independent)
$H_{1}$: 2개의 variable이 연관성이 있다. (dependent)
원인과 결과의 관계를 파악하는 것이 아니라, 그저 연관성의 존재 여부만을 조사한다.
d.f. : (number of rows -1) * (number of columns -1)
사람들이 가장 좋아하는 음식 종류는 성별과 연관이 있을까?
| 여자 | 남자 | Row total | |
| 닭발 | 5 | 2 | 7 |
| 치킨 | 3 | 2 | 5 |
| 국밥 | 1 | 5 | 6 |
| Column total | 9 | 9 | 18 |
test of homogenity와 계산 방식이 같다.
$\therefore$ p 값(0.002)이 유의 수준(0.05) 보다 작으므로 null hypothesis를 채택할 수 없다. 이 실험에서 성별은 좋아하는 음식 종류와 연관이 있다.
참고 자료
socratic.org/questions/what-is-the-difference-between-a-chi-square-test-of-independence-and-a-chi-squar#130607
spot.pcc.edu/~evega/twoWayTablesAndChiSquare.html
philschatz.com/statistics-book/contents/m47088.html
en.wikipedia.org/wiki/Chi-squared_test
'Research > Research methodology' 카테고리의 다른 글
| [디자인 연구 방법론 - t-test와 One-way ANOVA] 평균 비교 (0) | 2020.10.02 |
|---|---|
| [디자인 연구 방법론 - Basic] 0. 기초부터 다시보자 (0) | 2020.10.01 |
- 성차별
- 게티
- 성격특성
- 전월세대출
- 그리니치
- LA
- 학회
- lalaland
- 인생의발견
- 연구방법론
- 카카오뱅크
- san diego
- 부
- 인생의 발견
- 일상
- 페미니즘
- SanDiego
- SIGGRAPH
- MOCA
- 신한은행
- Sustainability
- Irvine
- 여행
- San Francisco
- 청년전세대출
- 성격의 탄생
- 성격심리학
- 미국
- santa barbara
- 라라랜드
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
